Az elején érdemes tisztázni pár elméleti dolgot, hogy mi fán terem a verifikáció, pontosabban elorejelzés verifikáció. Egyrészt szükség van elorejelzésekre, amiket verifikálunk, másrészt észlelésekre, amivel az elorejelzés jóságát ellenorizni tudjuk.
1. Bevezetés
Mi az a verifikáció?
Az elején érdemes tisztázni pár elméleti dolgot, hogy mi fán terem a verifikáció, pontosabban elorejelzés verifikáció. Egyrészt szükség van elorejelzésekre, amiket verifikálunk, másrészt észlelésekre, amivel az elorejelzés jóságát ellenorizni tudjuk. A pontosságot általában számmal/számokkal is jellemezzük.
A verifikáció célja
A verifikációs eredmények vizsgálatával lehetoség nyílik különbözo elorejelzések összehasonlítására és az elorejelzés folyamatának fejlesztésére is. Információt ad arról is, hogy egy döntési helyzetben mennyire lehet figyelembe venni az adott elorejelzést.
Különbözo célok összefoglalva:
- adminisztratív: monitorozás, elorejelzések összehasonlítása/kiválasztása
- tudományos: a modell hibáinak feltárása és kijavítása; az elorejelzési folyamat fejlesztése
- gazdasági: jobb döntéshozatal, automatikus döntéshozó rendszerek támogatása
A verifikáció minosége és értéke
Ez a két fogalom különbözo:
- Minoség (quality): valamilyen szempontból jól jelezzük elore az adott eseményt, pl. jó verifikációs méroszámokat kapunk.
- Érték (value): az elorejelzés alapján lehet-e jó döntést hozni? - ez az adott a felhasználótól függ. Például egy repülogéppilótát nem érdekel az, ha az éves csapadékmennyiséget jól jeleztük elore a repülési útvonal mentén.
Kérdések a verifkáció felhasználásához, értelmezéséhez:
- Milyen meteorológiai változót verifikáljunk? (pl. homérséklet, csapadék, szupercella elofordulása...)
- Milyen idobeli/térbeli felbontással vegyük figyelembe az adatokat? (pl. napi adatok, Magyarország)
- Milyen kategóriákat, küszöbértékeket használjunk? (pl. hideg/meleg, kis/nagy valószínuséggel)
- Milyen verfikációs méroszámot/méroszámokat használjunk? (pl. találati arány)
Ez függ az adott meteorológiai változó típusától is.
A verifikációs megfigyelési adatok tulajdonságai
A verifikációhoz felhasznált adatokkal kapcsolatban a következo szempontokat kell figyelembe venni:
- A mérési hiba miatt "sohasem tudjuk a teljes igazságot". A mérési hiba tulajdonságai az adatok forrásától függenek: méroállomások/földi észlelések, radar, muhold, modell elorejelzés, modell analízis
- A megfigyelési adatok függetlenek egymástól és az elorejelzéstol? Ha nem, akkor torzított eredményeket kaphatunk. Például egy modell analízisnél a függetlenség nem teljesül.
- Az elorejelzés és megfigyelés párosítása nem mindig egyszeru feladat. Fontos a reprezentativitás: az elorejelzés lehetoleg ugyanarra a helyre és idopontra legyen érvényes, mint ahol és amikor az eseményt is figyelembe vesszük. Néha interpoláció szükséges, rácspontok közötti értékek meghatározására.
Egy gondolatkísérlet erejéig képzeljük el, hogy a következo elorejelzést szeretnénk verifikálni: Lesz-e csapadék 16:27 perckor Kiskunlacházán? GFS esetén a csapadék elorejelzés 0.5 fokos rácspontokra és 3 óránként áll rendelkezésre. Megfigyelésként a 10 percenként frissülo radartérképet vesszük figyelembe. (Érdemes az olvasónak elgondolkodnia, hogy itt milyen problémák merülhetnek fel.)
A verifikációs eredmények megbízhatósága
- Ritka események esetén relatíve sok verifikációs adatra van szükség.
- A verifikációs méroszámok bizonytalanságának becsléséhez érdemes konfidencia intervallumokat meghatározni. Ezt úgy tehetjük meg, hogy a megfigyelési adatokat mesterségesen megváltoztatjuk, ezzel a megfigyelés hibáját próbáljuk reprezentálni. Több ilyen esetet leszimulálva megnézünk, hogyan szóródik a méroszám ennek hatására.
- Érdemes egyszerre több méroszámot megvizsgálni, ill. különbözo küszöbértékeket alkalmazni.
Verifikációs módszerek csoportosítása
Az elorejelzés természete lehet:
- determinisztikus: pl. 18 fok várható
- valószínuségi: pl. 10% eséllyel eso várható
- kvalitatív: szavakkal leírható, pl. szép ido várható (ezzel a továbbiakban nem foglalkozom)
Az elorejelzett érték tartománya szerint:
- bináris: igen/nem, pl. várható-e eso?
- multikategóriás, pl. hideg/átlagos/meleg ido várható
- folytonos, pl. maximális homérséklet
- objektum/esemény-alapú, pl. trópusi ciklon
Még lehet csoportosítani tér és ido tartománya szerint:
- idosor egy adott helyen, pl. maximális homérsékletek egy adott városban
- térbeli adatok egy adott idopontban, pl. légnyomástérkép
- tér- és idobeli adatok összesítése, pl. áltagos globális homérséklet-anomália egy adott hónapban
Kitéro - standard vs. tudományos verifikáció
Ebben a dokumentumban csak az ún. standard verifikációs módszereket fejtem ki részletesen. Ezek általában nagyszámú elorejelzés és észlelés összegzésével készült statisztikáknak foghatóak fel.
A másik típus az ún. tudományos vagy diagnosztikus verifikáció. Ezek magukban foglalják a térbeli adatok analízisét és az objektum-alapú módszereket (itt többdimenziós adatok feldolgozásáról is van szó). Fo céljuk az elorejelzett folyamat részleteibe belemenve az elorejelzés hibáinak felderítése.
Egy példa, amikor egy csapadékgóc elorejelzését verifikáljuk radar segítségével. Megnézzük, hogy a góc elorejelzett középpontja, területe, illetve maximális intenzitása mennyire tér el a valóságos, radarral mért csapadékgóc azonos tulajdonságaitól. A kapott eltérések alapján eldöntjük, elfogadható volt-e az elorejelzés.
Ezeket általában ember végzi, egyszeruen szemmel megállapítja az eltéréseket, aztán szubjektíve eldönti, hogy milyen volt az elorejelzés. Ez kevés adat esetén jól muködik, viszont ezek számának növekedésével egyre inkább szükség van automatizálására - ez az eredmény számszerusítése miatt sem egy utolsó szempont. A számítógéppel való kiértékelés bonyolultabb algoritmusokat igényel, mint egy egyszeru átlagolás vagy statisztika.
Ezek az eljárások jóval szerteágazóbbak, specifikusabbak, illetve adott esetben komplexebb matematikai módszereket alkalmaznak (különféle transzformációk, képfeldolgozás, fuzzy módszerek).
A standard verifikációnál maradva, az elorejelzés természete (determinisztikus/valószínuségi) és értéktartománya (bináris/multikategóriás/folytonos) szerint 6 kombináció lehetséges, de ezeket általában 4 csoportba szokták beosztani:
- Bináris-determinisztikus
- Multikategóriás-determinisztikus
- Folytonos-determinisztikus
- Valószínuségi elorejelzés (ezen belül lehet bináris, multikategóriás és folytonos)
2. Bináris-determinisztikus (igen/nem) elorejelzés
Itt az elorejelzés és a megfigyelés is mindössze két értéket vehet fel. Ez esetben 2x2, azaz 4 lehetséges eset van aszerint, hogy elorejeleztük-e az adott eseményt, és valóban bekövetkezett-e.
Több elorejelzést leverifikálva ezen esetek számát egy táblázatban összesíthetjük, aminek a neve kontingencia táblázat:
| Megfigyelés | |||
| igen | nem | ||
| Elorejelzés | igen | A | B |
| nem | C | D | |
Az esetek számának elnevezései:
- A: találatok száma (hits)
- B: téves riasztások száma (false alarms)
- C: elmulasztott események száma (misses)
- D: helyes negatív elorejelzések száma (correct negatives)
Az összes eset száma N:
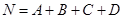 (1)
(1)
A sorok ill. oszlopok összegzésével meghatárózhatóak az elorejelzések ill. megfigyelések száma. Képezheto az esemény elofordulási gyakorisága (p), és az elorejelzés gyakorisága (q).
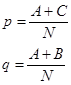 (2)
(2)
A fenti értékek egyszeru összegzésként szolgálnak. A négy fajta eset számaiból sokféleképpen képezheto olyan méroszám, amely az elorejelzés jóságát fejezi ki. A következokben a legismertebbeket sorolom fel.
2.1 Gyakran használt egyszerubb méroszámok
- Pontosság (accuracy): A leggyakrabban használt méroszám, ami megmondja, hogy az összes eset közül mekkora rész lett helyesen elorejelezve:
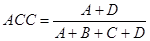 (3)
(3)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 1
Bizonyos esetekben ez a méroszám félrevezeto lehet, foleg amikor egy ritka eseményrol van szó. Erre egy jó példa, hogyha sohasem jelzünk elore tornádót, akkor is magas (valószínuleg 95%-nél nagyobb) ACC-ot fogunk kapni, mivel a tornádó elofordulási gyakorisága általában pár % körül van.
- Torzítás (bias): Ez a méroszám azt mondja meg, hogy mennyivel többször jeleztük elore az eseményt, mint ahogy az bekövetkezett.
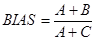 (4)
(4)
Értéktartomány: 0..8
Tökéletes elorejelzés esetén értéke: 1
Jelzi, hogy alul, vagy felülbecsültük az esemény bekövetkezési elofordulását. Arról viszont nem ad információt, hogy az egyes elorejelzések mennyire felelnek meg a tényleges bekövetkezéseknek.
- Találati arány (Sensitivity/True positive rate/Hit rate/Probability of detection): Egy másik gyakran használt méroszám, ami azt mondja meg, hogy a bekövetkezett események közül mekkora részt jeleztünk elore:
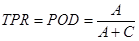 (5)
(5)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 1
Az "igen" elorejelzések számának növelésével egyszeruen javítható. Hátránya, hogy nem veszi figyelembe a téves riasztásokat, és érzékeny az esemény elofordulási gyakoriságára.
- Téves riasztás aránya (False alarm ratio): Megmondja, hogy az elorejelzések mekkora része téves riasztás:
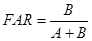 (6)
(6)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 0
Figyelembe veszi a téves riasztásokat, de az elmulasztott eseményeket nem. Érzékeny az esemény elofordulási gyakoriságára.
- Hamis pozitív arány (False positive rate/Probability of false detection): Azt mondja meg, hogy az esetek mekkora részében volt téves riasztás, amikor nem következett be az esemény:
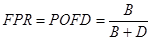 (7)
(7)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 0
Hasonlóan az elozohöz, figyelembe veszi a téves riasztásokat, de az elmulasztott eseményeket nem. Ha csökkentjük az "igen" elorejelzések számát, akkor egyszeruen javíthatjuk az értékét.
- Critical success index/Treat score: Azt mondja meg, hogy arányaiban mennyire jeleztük elore jól az esemény bekövetkezését azon esetek közül, amikor bekövetkezett az esemény, vagy pedig elorejeleztük azt.
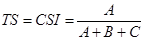 (8)
(8)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 1
Ez a méroszám figyelembe veszi mind a találatokat, a mulasztásokat és a téves riasztásokat is. Az elorejelzési hiba forrását nem különbözteti meg, és ez is érzékeny az esemény elofordulási gyakoriságára.
- F1 score: Hasonló a TS-hez (Treat score), felhasználja a találatokat, a mulasztásokat és a téves riasztásokat is.
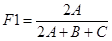 (9)
(9)
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 1
2.2 Gyakran használt bonyolultabb méroszámok
A bonyolultabb méroszámok tárgyalása elott érdemes tisztázni a véletlen elorejelzések fogalmát. Tegyük fel, hogy valaki úgy jelez elore egy adott jelenséget, hogy nem nézi meg az azt kiváltó feltételeket, azaz vakon jósol. Ha N eset van, akkor ebbol o q*N esetben jelzi elore a jelenséget, teljesen hasraütésszeruen (q az elorejezés gyakorisága). Ebben az esetben fel lehet írni, hogy hosszútávon a kontingencia táblázatban hova hány eset fog tartozni átlagosan az N esetbol:
| Megfigyelés | |||
| igen | nem | ||
| (Véletlen) Elorejelzés |
igen | p*q*N | (1-p)*q*N |
| nem | p*(1-q)*N | (1-p)*(1-q)*N | |
A p itt is az esemény elofordulási gyakoriságát jelenti. A fenti táblázatban felhasználtam az események függetlenségére vonatkozó szabályt, miszerint két független esemény valószínuségét a két esemény valószínuségének összeszorzásával kapjuk meg. Például: P(találat) = P(megfigyelés volt ÉS elorejelzés volt) = P(megfigyelés volt)*P(elorejelzés volt)
- Equitable Treat Score/Gilbert Skill Score: Az Treat Score továbbfejlesztett változata. A találatok számát korrigálja a véletlen találatok számával (Ar):
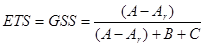 (10)
(10)
A véletlen találatokat megkaphatjuk, ha ránézünk a Táblázat 2-re, és vesszük a találatoknál levo értéket:
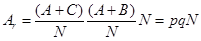
Azaz egy olyan fiktív, véletlenszeru elorejelzés találatait számoljuk itt ki, aminek a q rátája megegyezik az eredeti elorejelzésünkével. Más szóval, ha véletlenszeruen jeleztünk volna elore, akkor hány eseményt találtunk volna el.
Értéktartomány: -1/3..1
Tökéletes elorejelzés esetén értéke: 1
A nulla érték a véletlenszeru elorejelzés szintjének felel meg, a negatív pedig az annál rosszabb elorejelzésnek.
Ennek a méroszámnak egyetlen hátránya, hogy az elorejelzési hiba forrását nem különbözteti meg.
- True skill statistic/Hanssen and Kuipers discriminant/ Peirce's skill score: Azt mondja meg, mennyire szeparálja el egymástól az elorejelzés a bekövetkezett illetve a nem bekövetkezett események csoportját.
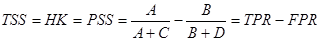 (11)
(11)
Értéktartomány: -1..1
Tökéletes elorejelzés esetén értéke: 1
Ez a méroszám a táblázat összes elemét felhasználja, és értéke nem függ az esemény elofordulási gyakoriságától. Az értelmezését ritka események esetén kissé nehezíti az a tény, hogy ekkor az elso tag (TPR) felülértékelodik, mivel a második tag nevezojében egy nagy szám szerepel, tehát FPR 0 körüli érték lesz.
- Heidke Skill Score: Ez a pontosság (ACC) egy módosított változatának is felfogható, a különbség az, hogy a "véletlenül jól sikerült" elorejelzéseket levonjuk a számlálóban és a nevezoben is.
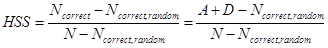 (12)
(12)
A "véletlenül jól sikerült" elorejelzések számát hasonlóan kapjuk meg, mint az ETS-nél, viszont itt nem csak az A mezore számoljuk ki a véletlen találatokat, hanem hozzávesszük a D mezo véletlen találatait is (amikor nem jeleztük elore az eseményt ÉS nem is következett be), lásd Táblázat 2:
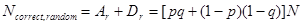
Értéktartomány: -8..1
Tökéletes elorejelzés esetén értéke: 1
A 0 érték itt is a véletlenszeru elorejelzéseket írja le, amikor a számláló nulla, a negatív értékek pedig az ennél még rosszabb elorejelzéseket.
- Odds ratio skill score: Információt ad arról, hogy az elorejelzés mennyivel jobb a véletlen tippelésnél.
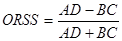 (13)
(13)
Értéktartomány: -1..1
Tökéletes elorejelzés esetén értéke 1, a nulla érték a véletlen elorejelzéseket reprezentálja.
Független a sor és oszlopösszegektol.
- Korrelációs együttható (általános definíció)
Az érthetoség és az egyszerubb felírás érdekében érdemes eloször bevezetni az átlagot és a szórást. Az elorejelzések és megfigyelések átlaga:
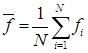
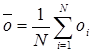
A szórások definíciója az elorejelzésekre és megfigyelésekre:
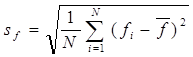
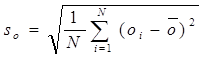
Ezekkel a mennyiségekkel a korrelációs együttható kifejezése a következo:
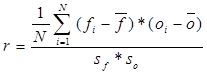 (14)
(14)
Értéktartomány: -1..+1
Tökéletes elorejelzés esetén értéke: 1
Ennek a számnak szemléletes jelentése az, hogy a megfigyelés-elorejelzés pontokat 2 dimenzióban felrajzolva mennyire vagyunk közel egy egyeneshez. Ez az egyenes bárhol lehet, (14) az eltolásra nem érzékeny (pl. ha az összes elorejelzett értékhez hozzáadunk 10-et, ugyanazt az értéket kapjuk). Emellett érzékeny a kiugró adatokra.
- Korrelációs együttható/Phi coefficient/Matthews correlation coefficient (definíció bináris eseményekre):
Az elozo képletet (14) bináris eseményekre alkalmazva, a kontingencia táblázat elemeivel kifejezve:
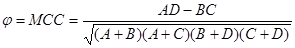 (15)
(15)
Figyelembe veszi a táblázat összes értékét. Hátránya, hogy viszonylag bonyolult kiszámolni.
- Skill-score: Ez egy általános képlet, amely bármelyik S méroszámra alkalmazható:
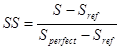 (16)
(16)
ahol Sref a referencia elorejelzés pontszáma, Sperfect a tökéletes elorejelzés pontszáma. A referencia elorejelzés lehet pl. véletlenszeru tippelés, vagy klimatológiai átlag. A SS fo tulajdonsága az, hogy a tökéletes elorejelzés esetén értéke 1, és elmondhatjuk, hogy pozitív érték esetén jobbak vagyunk a referencia elorejelzésnél, negatív érték esetén viszont rosszabbak.
2.3 A méroszámok kiválasztása
Felvetodhet a jogos kérdés, milyen méroszámot használjunk egy verifikációhoz? Több szempontot figyelembe lehet venni a kiválasztásnál:
- van egy véges minimum és maximum értéke
- a tökéletes elorejelzés esetén veszi fel a maximumértékét
- a legrosszabb elorejelzés esetén veszi fel a minimumértékét
- a "véletlen"/klimatológiai átlag elorejelzést ne díjazza, és ugyanaz legyen a várható értéke (például nulla). Ennek speciális esetei az olyan elorejelzések, amelyek szerint egy esemény mindig vagy soha sem következik be (nyilván ezek sem lehetnek jobbak a véletlen elorejelzésnél).
- az adott elorejelzést módosítva a véletlen elorejelzés irányába (ezt nevezzük kertelésnek) a méroszám lehetoleg ne javuljon
- az esemény gyakoriságától ne függjön
- ritka esemény esetén is informatív maradjon
Az elso három feltétel azt a célt szolgálja, hogy a különbözo elorejelzések összehasonlíthatóak maradjanak. A negyedik és ötödök pedig arra vonatkozik, hogy a tudást nem reprezentáló elorejelzések kevesebb pontot kapjanak.
Az elso 6 követelményt a TSS teljesíti, az MCC pedig az elso 5-öt.
Ha az 1-es vagy a 3-as feltételtol eltekintünk, akkor a HSS és az ETS is elfogadhatóan jó méroszámnak tekintheto.
Az ORSS is egy elfogadható méroszám - hasonlóan a TSS-hez - de abban az esetben, ha a táblázat bármelyik eleme nullához közeli, bizonytalan értéket ad.
Az utolsó feltételt az itt leírt méroszámok közül egyik sem teljesíti. (Létezik egyébként ezt teljesíto méroszám, pl. az ún. Symmetric Extreme Dependency Index, amit ebben a cikkben nem említek meg részletesebben.)
2.4 Elorejelzések összehasonlítása
Bár az (A,B,C,D) számnégyes egyértelmuen leírja az elorejelzések tulajdonságait, ezek alapján nehéz több elorejelzést összehasonlítani. Érdemes ezért különbözo csoportokra bontani az eseteket, például az események bekövetkezése szerint.
A ún. esemény-alapú felosztáshoz (likelihood-base rate factorization) a következo mennyiségeket lehet származtatni:
- N: összes eset száma
- p: az esemény elofordulási gyakorisága (tehát N*p esetben történt meg az esemény, és ezek száma A+C)
- TPR, FPR: a méroszámoknál már megismert találati arány és hamis pozitív arány (mindketto az elorejelzett esetek részarányát jelenti, az egyik a bekövetkezett, a másik pedig a nem bekövetkezett események csoportjában, lásd (5) és (7))
(Emellett létezik elorejelzés-alapú felosztás is, erre itt nem térek ki, mivel az nehezen használható összehasonlításhoz)
A kontingencia táblázat értékeit a következo módon lehet értelmezni a fenti szétbontás segítségével (a nyilak alatt a megfelelo arányok szerepelnek):
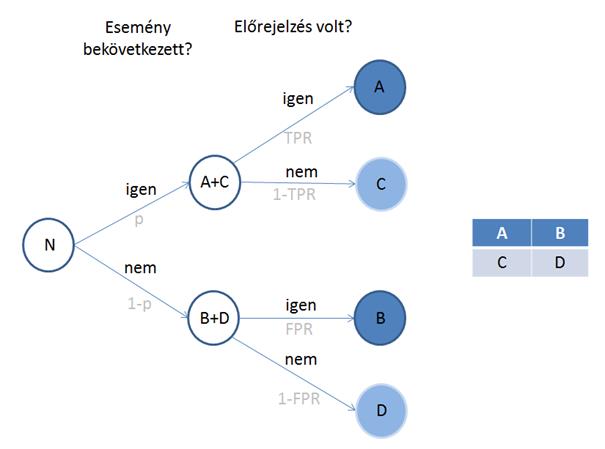
Tehát ez is 4 olyan szám, ami egyértelmuen leírja az elorejelzéseket. Amennyiben az esetek száma, illetve még az események adathalmaza sem változik, akkor N és p állandó, és ezért elég csak a TPR-t és FPR-t vizsgálni különbözo elorejelzések összehasonlításához. Ezt egy 2 dimenziós grafikonon szokás ábrázolni:
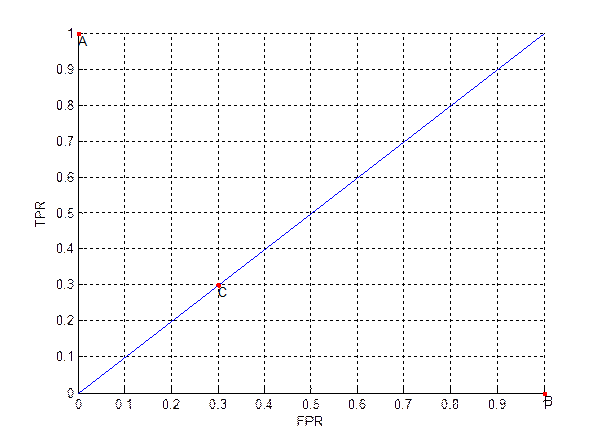
2. ábra
Minél nagyobb a TPR, és minél kisebb az FPR, annál jobb az elorejelzés. Az "A" pont a tökéletes elorejelzést írja le. A "B" ezzel szemben a leheto legrosszabb elorejelzést mutatja.
A "C" pont az átlón helyezkedik el, ami a semleges elorejelzéseket írja le. Ezek egyenértékuek a véletlen elorejelzésekkel, és nem hordoznak ahhoz képest plusz információt. A véletlen elorejelzés azt jelenti, hogy mind a bekövetkezett, mind pedig a nem bekövetkezett események esetében is arányaiban nézve ugyanannyiszor adunk ki elorejelzést. Ez más szóval annyit jelent, hogy a TPR és FPR értéke megegyezik.
Az átló felett elhelyezkedo elorejelzésekre azt mondhatjuk, hogy jobbak, mint a "véletlen" elorejelzés. Minél közelebb vagyunk az A ponthoz, annál jobbnak tekintheto az elorejelzés.
2.5 Bináris esemény elorejelzése folytonos segédváltozóval
A matematikai megfogalmazás általánosan:
A bináris eseményt egy folytonos változó (x) segítségével jelzünk elore. A folytonos elorejelzést eloször valahogyan igen/nem információvá kell átalakítani. A legegyszerubb eset az, ha az elorejelzés kimenetét egy küszöbérték (t) segítségével döntjük el. Ha x>=t, akkor igent, ha x<t, akkor nemet mondunk. Természetesen ennek a döntésnek más lehetoségei is vannak (az x egy bizonyos tartományban/tartományokban van stb.)
Egy elméleti példa kedvéért tegyük fel, hogy elore akarjuk jelezni a szupercellákat egy paraméter segítségével. Szeretnénk meghatározni egy küszöbértéket, amely felett azt tudjuk mondani, hogy inkább lehet szupercella.
Ebben a példában az x paraméter -15 és +15 között változik. A megfigyelés szerint az x változónak két csoportját lehet vizsgálni, aszerint, hogy a szupercella bekövetkezett, avagy nem következett be. Tegyük fel, hogy ez az x paraméter következo két elméleti eloszlással rendelkezik:
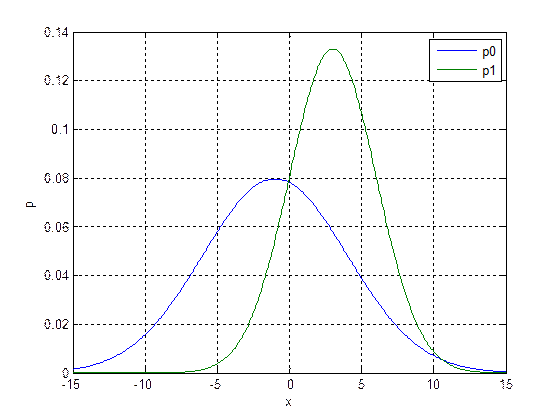
3. ábra
Látható, hogy a szupercellák nagy része 0 és 5 közötti paraméter érték körül található, míg a sima zivatarok inkább 0 közelében helyezkednek el. Kérdés, hogyan határozzuk meg a küszöbértéket?
Az elozo fejezetben leírt ábrázolást alkalmazva, felrajzolhatjuk az egyes küszöbértékhez tartozó pontokat a TPR-FPR térben, ezt ROC görbének hívjuk (receiver operating characteristic):
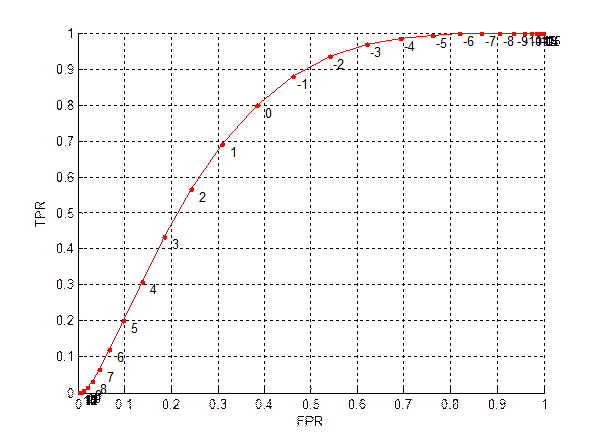
4. ábra
A görbét megvizsgálva egy 0 körüli érték tunik a legjobbnak, hiszen ez a rész helyezkedik el a tökéletes elorejelzés pontjához a legközelebb.
Általános módszer:
- különbözo küszöbértékekre meghatározzuk a kontingencia táblázatot
- kiválasztunk egy verifikációs méroszámot, és kiszámoljuk az összes táblázatra
- kiválasztjuk azt a küszöbértéket, amely a legjobb méroszámmal bír
Ha ismerjük már a feltételes eloszlásokat, azaz a p0(x) és p1(x) függvényeket, azokból egyszeruen kiszámolhatóak a TPR(x) és FPR(x) függvények. Ez esetben nem kell kontingencia táblázatokkal számolni. Ha a fenti példánál maradunk, és a TSS = TPR-FPR értékkel számolunk, megmutatható, hogy az optimális küszöbérték a p0 és p1 görbe metszéspontjánál helyezkedik el.
Egyes méroszámok az esemény bekövetkezési valószínuségétol (p) is függenek, ezért befolyásolják az optimális küszöbérték elhelyezkedését.
2.6 Költség alapú megközelítés
A cél ebben az esetben az, hogy meghatározzuk az elorejelzés várható költségét. Ezt úgy tehetjük meg, hogy mind a négy lehetséges esethez hozzárendelünk egy költséget. Ezt egy költségmátrixszal ábrázolhatjuk:
| Megfigyelés | |||
| igen | nem | ||
| Elorejelzés | igen | cfo | cf |
| nem | co | 0 | |
Amikor nem következik be az esemény, és nem is jeleztük azt elore, akkor a költséget nullának feltételezhetjük. A téves riasztás költségét viszont már figyelembe vesszük egy nem nulla értékkel. A legnagyobb általában az elmulasztott esemény költsége. A találat költsége ennél jóval kisebb, mivel meg tudjuk elozni a károk egy részét. Elméleti problémáknál ez nullának veheto, de általában egy valós eseménynél ez nem nulla, gondoljunk például a tornádókra.
A várható költség kifejezése, elofordulási arányok felhasználásával:
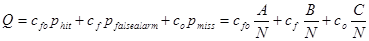 (17)
(17)
Ennek egy speciális esete, amikor a találathoz nulla költséget rendelünk, ami azt jelenti, hogy csak a hibás elorejelzéseket vesszük számításba. Ekkor a két hiba együtthatója határozza meg, melyiket súlyozzuk fel jobban.
Amennyiben a két fajta hibát egyenlo súllyal vesszük figyelembe, akkor (1-ACC)-val (azaz a hibás elorejelzések arányával) kapunk egy arányos mennyiséget.
Általában ez a fajta költség, mint méroszám csak az elso hármat teljesíti a méroszámok kiválasztásánál leírt feltételek közül, de arra jól használható, hogy megindokoljuk egy elorejelzés létjogosultságát gazdaságilag. Ugyanis összehasonlíthatjuk az elorejelzés nélküli költséggel, ami a következo képlettel számolható (ekkor az összes bekövetkezett esemény a "miss" kategóriába sorolható):
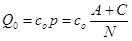
A várható költség felírható TPR és FPR segítségével is:
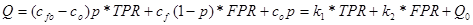 (18)
(18)
Megjegyzés: A szakirodalomban az ún. cost-loss model-t szokták megemlíteni, ami a fenti költségek egy hasonló felírását alkalmazza. Ez a várható költségbol gyakorlatilag egy skill-score-t képez (lásd (16)) a klimatológiai információt referenciának használva, és ezt relatív értéknek nevezi el. Ezt itt nem tárgyalom részletesebben.
3. Multikategóriás-determinisztikus elorejelzés
Ebben az esetben kettonél több elorejelzett kategória van. Ezt is ábrázolhatjuk táblázatban, a kontingencia-táblázathoz hasonlóan. Ha K darab kategóra van, akkor:
| Megfigyelés | |||||
| Kategória 1 | Kategória 2 | ... | Kategória K | ||
| Elorejelzés | Kategória 1 | n(1,1) | n(1,2) | ... | n(1,K) |
| Kategória 2 | n(2,1) | n(2,2) | ... | n(2,K) | |
| ... | ... | ... | ... | ... | |
| Kategória K | n(K,1) | n(K,2) | ... | n(K,K) | |
Az n(i,j) jelöli azon esetek számát, amikor az i. kategóriát jeleztük elore, és a j. kategória következett be.
A foátlóbeli számok (n(i,i)) jelölik azokat az eseteket, amikor helyesen jeleztük elore az adott eseményt, a foátlón kívüli esetek pedig a hibás elorejelzéseket reprezentálják. Látható, hogy nagyon sokféle hiba lehetséges, így nehéz egy darab méroszámmal kifejezni az elorejelzés jóságát. Ennek ellenére van pár olyan méroszám, amit bináris esetrol ki lehet terjeszteni több kategóriás elorejelzésre.
- Pontosság (accuracy): Az összes eset mekkora része lett helyesen elorejelezve, azaz mennyi elem van a foátlóban:
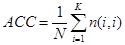 (19)
(19)
ahol N a táblázatban szereplo kategóriák száma.
Értéktartomány: 0..1
Tökéletes elorejelzés esetén értéke: 1
Itt is elmondható, hogy ez a legegyszerubb mérték, bár félrevezeto lehet abban az esetben, ha a kategóriák nem egyenletesen oszlanak el (azaz gyakoriságuk nagyon eltéro).
- True skill statistic/Hanssen and Kuipers discriminant/ Peirce's skill score:
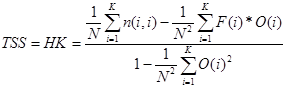 (20)
(20)
Értéktartomány: -1..1
Tökéletes elorejelzés esetén értéke: 1
Ez a méroszám felhasználja a sor- és oszlopösszegeket. Az i. sor összege F(i), azaz az i. kategória elorejelzések száma, míg az i. oszlop összege O(i), azaz az i. kategória megfigyelések száma. A TSS arról ad információt, hogy az elorejelzésünk mennyivel jobb a véletlen tippelésnél, normalizálva a tökéletes elorejelzéssel. Ugyanis a számláló a véletlen tippeléshez képesti javulást írja le, a nevezo pedig gyakorlatilag ugyanez a kifejezés egy tökéletes elorejelzés esetében (ekkor az elso tag 1, mert csak a foátlóban szerepelnek elemek, ill. a második tagban a sor és oszlopösszegek megegyeznek, F(i)=O(i))
- Heidke Skill Score:
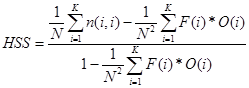 (21)
(21)
Értéktartomány: -8..1
Tökéletes elorejelzés esetén értéke: 1
A képlet hasonló, mint a TSS esetén, csak a nevezoben van eltérés.
Egyéb módszerek
Ezen kívül vannak még a fentieknél bonyolultabb, de gyakran használt méroszámok (pl. Gerrity score), amit itt nem tárgyalok.
Egy másik verifikációs módszer a K darab kategóriára az, hogy verifikációt felbontjuk K-1 darab bináris (igen/nem) verifikációra - a fenti táblázatból K-1 darab 2x2-es táblázatot gyártunk úgy, hogy "elvágjuk" azt egy kategória-elválasztó vonalnál függolegesen és vízszintesen is, és összegezzük a számokat az így létrejövo 4 tartományban.
Ezt sem tárgyalom részletesebben ezen keretek között.
3. Összefoglalás
Ebben a tudományos cikkben a determinisztikus, kategorikus (diszkrét értéku) elorejelzések verifikációját foglaltam össze, aminek két fo része a kétértéku (bináris) illetve a többértéku elorejelzések voltak. A következo cikkekben a folytonos értéktartományú és a valószínuségi elorejelzések verifikációját fogom kifejteni. Szó lesz ezen kívül a 2014-es év konvektív elorejelzéseinek verifikációs eredményeirol is.
Bondor Gyula